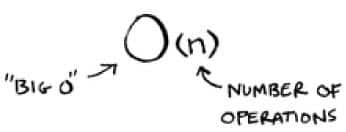La Notación Big O o Big O Notation es una forma de describir el rendimiento o la complejidad de un algoritmo. Se utiliza para evaluar cuánto tiempo o espacio requerirá un algoritmo a medida que crece el tamaño de los datos de entrada.

¿Como funciona?

La Notación Big O se representa usando la letra “O” seguida de una función que describe la relación entre el tamaño del problema y la cantidad de recursos utilizados. Siendo la “n” el numero de operaciones realizadas en dicho algoritmo.

Ilustración del libro "grokking algorithms"

Por ejemplo, O(n) indica que el algoritmo tiene un tiempo de ejecución lineal, lo que significa que la función crece proporcionalmente al tamaño del problema.

Tipos de Notación Big O

• O(1): Indica que el algoritmo tiene un tiempo de ejecución constante. Esto significa que el tiempo de ejecución no depende del tamaño del problema.

No importa si el problema tiene 10 elementos o 10,000 elementos, el algoritmo tomará aproximadamente la misma cantidad de tiempo para ejecutarse.

Es considerado el caso ideal de eficiencia, ya que el tiempo de ejecución es constante y no se ve afectado por el tamaño del problema.

• O(n): Indica que el algoritmo tiene un tiempo de ejecución lineal. Esto significa que el tiempo de ejecución aumenta de manera proporcional al tamaño del problema.

Si el tamaño del problema se duplica, el tiempo de ejecución también se duplicará. Por ejemplo, si se tiene una lista de n elementos y se recorre uno por uno, el tiempo de ejecución será proporcional al número de elementos en la lista. Es común encontrar algoritmos con esta complejidad en operaciones de búsqueda y recorrido lineal.

• O(log n): Indica que el algoritmo tiene un tiempo de ejecución logarítmico. Esto significa que el tiempo de ejecución aumenta de forma logarítmica a medida que el tamaño del problema aumenta.

En otras palabras, a medida que el tamaño del problema se duplica, el tiempo de ejecución solo aumenta en una cantidad constante.

Este tipo de complejidad se encuentra comúnmente en algoritmos de búsqueda binaria y estructuras de datos como árboles balanceados. Los algoritmos con complejidad logarítmica son considerados muy eficientes.

• O(n^2): Indica que el tiempo de ejecución del algoritmo es cuadrático. Esto significa que el tiempo de ejecución aumenta cuadráticamente con el tamaño del problema.

Si el tamaño del problema se duplica, el tiempo de ejecución se incrementará aproximadamente en cuatro veces. Algoritmos que involucran dos bucles anidados suelen tener esta complejidad. Es importante tener cuidado con esta complejidad, ya que para tamaños de problema grandes puede llevar a un tiempo de ejecución significativo.

• O(2^n): Indica que el tiempo de ejecución del algoritmo es exponencial. Esto significa que el tiempo de ejecución aumenta rápidamente a medida que el tamaño del problema crece.

Por cada elemento adicional en el problema, el tiempo de ejecución se duplica. Los algoritmos con esta complejidad son considerados ineficientes y pueden volverse impracticables para tamaños de problemas moderadamente grandes. Se deben buscar alternativas más eficientes cuando se enfrenta a algoritmos con esta complejidad.

• O(n!): Indica que el tiempo de ejecución del algoritmo es factorial. Esto significa que el tiempo de ejecución aumenta de manera factorial con el tamaño del problema.

La complejidad factorial es la peor de todas, ya que implica que el tiempo de ejecución crece de manera exponencial con cada elemento adicional.

Los algoritmos con esta complejidad son extremadamente ineficientes y generalmente no son viables para problemas de tamaño moderado o grande. Se deben buscar enfoques alternativos o algoritmos más eficientes para resolver este tipo de problemas.

• O(n log n): Indica que el tiempo de ejecución del algoritmo tiene una complejidad n log n. Esto significa que el tiempo de ejecución aumenta de forma proporcional al producto del tamaño del problema y el logaritmo del tamaño del problema.

Es común encontrar esta complejidad en algoritmos de ordenación eficientes, como el algoritmo Quicksort y el algoritmo Merge Sort. Aunque es más eficiente que una complejidad cuadrática (O(n^2)), aún es menos eficiente que una complejidad lineal (O(n)) o logarítmica (O(log n)). Los algoritmos con esta complejidad son utilizados para ordenar o realizar operaciones en conjuntos de datos de tamaño moderado a grande.

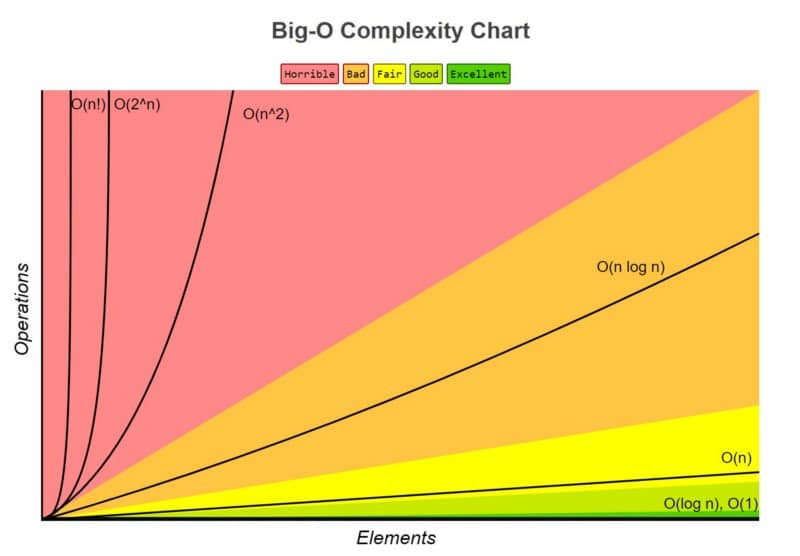
¡Veamos una gráfica para ver como se representan estos tipos de notación!

Gráfica del libro "grokking algorithms"

En esta gráfica, podemos observar que los algoritmos ubicados en la zona roja son los menos eficientes. En la zona naranja, aunque mejoran en comparación con la zona roja, siguen siendo considerados menos eficientes. Los algoritmos que se encuentran en la zona amarilla muestran una eficiencia normal, mientras que los situados en la zona verde clarito se consideran más eficientes. Por último, los mejores algoritmos se encuentran en la zona verde.

Conclusiones

En conclusión, la notación Big O es una herramienta fundamental para describir la complejidad y el rendimiento de los algoritmos. A través de esta notación, podemos evaluar cómo varía el tiempo de ejecución o el uso de recursos a medida que crece el tamaño del problema.